State of Valhalla
This is the second of three documents describing the current State of Valhalla. The first is The Road to Valhalla; the third is The JVM Model.
This document describes the directions for the Java language charted by Project Valhalla. (In this document, we use “currently” to describe the language as it stands today, without value classes or extended primitives.)
Valhalla started with the goal of providing user-programmable classes which could be flat and dense in memory. Numerics are one of the motivating use cases, but adding new primitive types directly to the language has a very high barrier. As we learned from Growing a Language there are infinitely many numeric types we might want to add to Java, but the proper way to do that is as libraries, not as language features.
Primitive and reference types in Java today
Java currently has eight built-in primitive types. Primitives represent pure values; any int value of “3” is equivalent to (and indistinguishable from) any other int value of “3”. Values have no canonical location, and so are freely copyable. With the exception of the unusual treatment of NaN values for float and double, the == operator performs a substitutability test — it asks “are these two values the same value?”
Java also has objects, and each object has a unique object identity. Because of identity, objects are not freely copyable; each object lives in exactly one place (at any given time), and to access its state we have to go to that place. But we mostly don’t notice this because objects are not manipulated or accessed directly, but instead through object references. Object references are also a kind of value — they encode the identity of the object to which they refer, and the == operator on object references asks “do these two references refer to the same object?” Accordingly, object references (like other values) can be freely copied, but the objects they refer to cannot.
Primitives and objects differ in almost every conceivable way:
| Primitives | Objects |
|---|---|
| No identity (pure values) | Identity |
== compares values |
== compares object identity |
| Built-in | Declared in classes |
| Not nullable | Nullable |
| No members (fields, methods, constructors) | Members (including mutable fields) |
| No supertypes or subtypes | Class and interface inheritance |
| Accessed directly | Accessed via object references |
| Default value is zero | Default value is null |
| Arrays of primitives are monomorphic | Arrays are covariant |
| Tearable under race | Initialization safety guarantees |
| Convertible to polymorphic objects | Polymorphic |
The design of primitives represents various tradeoffs aimed at maximizing performance and usability of the primitive types. Reference types default to null, meaning “referring to no object”; primitives default to a usable zero value (which for most primitives is the additive identity). Reference types provide initialization safety guarantees against a certain category of data races; primitives allow tearing under race for larger-than-32-bit values. We could characterize the design principles behind these tradeoffs as “make objects safer, make primitives faster.”
The following figure illustrates the current universe of Java’s types. The upper left quadrant is the built-in primitives; the rest of the space is reference types. In the upper-right, we have the abstract reference types — abstract classes, interfaces, and Object (which, though concrete, acts more like an interface than a concrete class). The built-in primitives have wrappers or boxes, which are reference types.
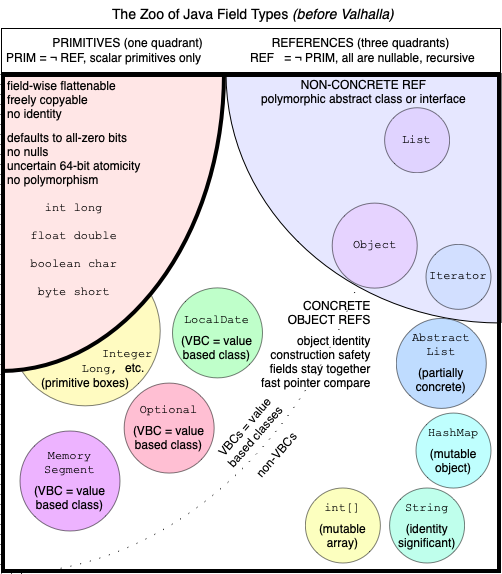
Valhalla aims to unify primitives and objects so that primitive-like types can be declared with classes, while maintaining the special runtime characteristics primitives have. Moreover, while everyone likes the flatness and density that user-definable value types promise, in some cases we want them to be more like classical objects (nullable, non-tearable), and in other cases we want them to be more like classical primitives (trading some safety for performance). Over time, it has become clear that there is no one-size-fits-all answer.
Value classes: separating references from identity
Many of the impediments to optimization that Valhalla seeks to remove center around unwanted object identity. The primitive wrapper classes have identity, but not only is this identity not directly useful, it can be a source of bugs. (For example, due to caching, Integers can be accidentally compared correctly with == just often enough that people keep doing it.) Similarly, value-based classes such as Optional have no need for identity, but pay the costs of having identity anyway.
Our first step is allowing class declarations to explicitly disavow identity, by declaring themselves as value classes. The instances of a value class are called value objects.
value class ArrayCursor<T> {
T[] array;
int offset;
public ArrayCursor(T[] array, int offset) {
this.array = array;
this.offset = offset;
}
public boolean hasNext() {
return offset < array.length;
}
public T next() {
return array[offset];
}
public ArrayCursor<T> advance() {
return new ArrayCursor(array, offset+1);
}
}This says that an ArrayCursor is a class whose instances have no identity. As a consequence, they must give up the things that depend on identity; the class and its fields are implicitly final.
But, value classes are still classes, and can have most of the things classes can have — fields, methods, constructors, type parameters, superclasses (with some restrictions), nested classes, class literals, interfaces, etc. The classes they can extend are restricted: Object or abstract classes with no fields, empty no-arg constructor bodies, no other constructors, no instance initializers, no synchronized methods, and whose superclasses all meet this same set of conditions. (Number is an example of such a class.)
Value class types are still reference types; we refer to value objects via object references. This means that object references can refer to either identity objects or value objects; for the types in the upper-right quadrant (interfaces, abstract classes, and Object), references to these types might refer to either an identity object or a value object. (Historically, JVMs were effectively forced to represent object references with pointers; for references to value objects, JVMs now have more flexibility.)
Because they are reference types, value class types are nullable, their default value is null, and loads and stores of references are atomic even in the presence of data races, providing the initialization safety we are used to with classical objects.
Because they are values, == compares value objects by state rather than identity. This means that value objects, like primitives, are freely copyable; we can explode them into their fields and re-aggregate them into another value object, and we cannot tell the difference. (Because they have no identity, some identity-sensitive operations, such as synchronization, produce runtime exceptions.)
Value classes take aim at the first two lines of the table of differences above; rather than identity being a property of all objects, it becomes a declared property of classes, such as finality. By allowing classes that don’t need identity to exclude it, we free the runtime to make better layout and compilation decisions — and avoid a whole category of bugs.
In looking at the code for ArrayCursor, we might mistakenly assume it will be inefficient, as each loop iteration appears to allocate a new cursor:
for (ArrayCursor<T> c = Arrays.cursor(array);
c.hasNext();
c = c.advance()) {
// use c.next();
}One should generally expect here that no cursors are actually allocated. Because an ArrayCursor is just its two fields, these fields will get hoisted into registers, and the constructor call in advance will typically compile down to incrementing one of these registers.
Migration
The JDK (as well as other libraries) has many value-based classes, such as Optional and LocalDateTime. Value-based classes adhere to the semantic restrictions of value classes, but are still identity classes — even though they don’t want to be. Value-based classes can be migrated to true value classes simply by redeclaring them as value classes. This is both source- and binary-compatible.
We plan to migrate many value-based classes in the JDK to value classes. Additionally, the primitive wrappers can be migrated to value classes as well, making the conversion between int and Integer cheaper. (In some cases, this may be behaviorally incompatible for code that synchronizes on the primitive wrappers. JEP 390 has supported both compile-time and runtime warnings for synchronizing on primitive wrappers since Java 16.)

Value records
While records have a lot in common with value classes — they are final and their fields are final — they are still identity classes. Records embody a tradeoff: give up on decoupling the API from the representation, and in return get various syntactic and semantic benefits. Value classes embody another: give up identity, and get various semantic and performance benefits. If we are willing to give up both, we can get both sets of benefits:
value record NameAndScore(String name, int score) { }Value records combine the data-carrier idiom of records with the improved scalarization and flattening benefits of value classes.
In theory, it would be possible to apply value to certain enums as well, but this is not currently possible because the java.lang.Enum base class that enums extend does not meet the requirements for superclasses of value classes (it has fields and non-empty constructors).
Identity-sensitive operations
Certain operations are currently defined in terms of object identity. Some of these, like equality, can be sensibly extended to cover all object instances. Others, like synchronization, will become partial. Identity-sensitive operations include:
-
Equality. Two value objects are
==if they are of the same type, and each of their fields are pairwise equal, where equality is given by==for primitives (exceptfloatanddouble, which are compared “bitwise” withFloat::equalsandDouble::equalsto avoid anomalies withNaNand-0.0),==for references to identity objects, and recursively with==for references to value objects. In no case is a value object ever==to an identity object. -
System::identityHashCode. The main use of
identityHashCodeis in the implementation of data structures such asIdentityHashMap. We can extendidentityHashCodein the same way we extend equality — deriving a hash on primitive objects from an implementation-defined mixing function on all the fields, or perhaps on a partial subset. -
Object methods. The default implementations of
toString,equals, andhashCode, as defined by the classObject, are based on object identity. They can be modified, consistent with==, to be based on the object’s field values instead. -
Synchronization. This becomes a partial operation. If we can statically detect that a synchronization will fail at runtime (including declaring a
synchronizedmethod in a value class), we can issue a compilation error; if not, attempts to lock on a value object results inIllegalMonitorStateExceptionat runtime. This is justifiable because it is intrinsically imprudent to lock on an object for which you do not have a clear understanding of its locking protocol; locking on an arbitraryObjector interface instance is doing exactly that. -
Weak references. If we made creating weak references a partial operation on
Object, weak references would become almost useless, as every class that wants to maintain some sort of weak data structure would have to bifurcate into separate paths for identity and value objects. (This would be similar to partializingidentityHashCode.) Weak references to value objects that contain no references to identity objects should never be cleared; weak references to value objects that contain references to identity objects should be cleared when those objects are no longer strongly reachable. -
Serialization. Serialization currently uses object identity to preserve the topology of an object graph. This generalizes cleanly to value objects, because
==on value objects treats two identical copies of a value object as equal. So any observations we make about topology prior to serialization are consistent with those after deserialization.
Identifying identity
To distinguish between value and identity types at compile time, and between value and identity objects at run time, we introduce two restricted interfaces, IdentityObject and ValueObject. IdentityObject is implicitly implemented by identity classes; ValueObject is implicitly implemented by value classes; no class can implement both. This enables us to write code that dynamically tests for object identity before performing identity-sensitive operations:
if (x instanceof IdentityObject) {
synchronized(x) { ... }
}It also statically reflects the requirement for identity in variable types (and generic type bounds):
static void runWithLock(IdentityObject lock, Runnable r) {
synchronized (lock) {
r.run();
}
}If an interface or abstract class implements IdentityObject or ValueObject, this serves as a constraint that it may only be extended by the appropriate sort of class.
What about Object?
The root class Object poses an unusual problem, in that every class must extend it directly or indirectly, but it itself is (currently) an identity class, and it is common to use new Object() as a way to obtain a new object identity for purposes of locking. If Object were to implement IdentityObject, then primitive classes could not extend Object (and therefore could not interoperate with dynamically typed libraries such as reflection). We address this problem by treating Object like we do interfaces and certain abstract classes — they can be extended by both identity and primitive classes — but redefine the idiom new Object() to evaluate to a fresh instance of an anonymous identity subclass of Object.
Primitive classes
Value classes allow developers to give up one thing — identity — and gain a host of performance and predictability benefits. They are an ideal replacement for many of today’s value-based classes, fully preserving their semantics (except for the accidental identity these classes never wanted). But they represent only one point on a spectrum of tradeoffs between abstraction and performance, and other desired use cases — such as numerics — may want a different set of tradeoffs.
Specifically, value classes still use reference types. This means they are nullable, and therefore must account for null somehow in their representation, which may have a footprint cost. Similarly, value classes offer the initialization safety guarantees that we’ve come to expect from classes, which also has a cost to preserve, compared to primitives. For certain use cases, we may desire to additionally give up something else to gain the maximum flatness and density possible — and that something else is reference-ness.
Primitive classes allow us to define new primitive types, with essentially the same runtime behavior as the basic primitives (int, double, etc.).
primitive class Point implements Serializable {
int x;
int y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
Point scale(int s) {
return new Point(s*x, s*y);
}
}A primitive class is a special value class whose instances can be represented as values of a primitive type. The name of the class (Point) is also the name of the primitive type. Users of the primitive type can expect familiar primitive semantics and performance — for example, the primitive type cannot be null.
A primitive class declaration is subject to the same constraints as value class declarations (e.g., the instance fields are implicitly final). Additionally, primitive type circularities in instance field types are not allowed — flattened instances must not contain other instances of the same type.
Unlike the basic primitives, primitive types declared with classes can be used as receivers to access the fields and invoke the methods of the class (modulo accessibility):
Point p = new Point(1, 2);
assert p.x == 1;
p = p.scale(2);
assert p.x == 2;The == operator can be used to compare two primitive values of the same type; it performs a pairwise comparison of the values’ fields, just as for value objects.
assert p.scale(2) == new Point(2, 4);Polymorphism
Primitive classes can extend abstract classes and implement interfaces. Yet primitive values are bare, untagged data. How can they support polymorphism? The answer is that instances of a primitive class can also be represented as value objects, like instances of any other value class. These objects support subtyping, virtual dispatch, etc.
Unlike most classes, a primitive class declares two types: the primitive type (Point) and a reference type (Point.ref). Both types have the same members. Instances can be operated on in either form, as needed, and freely converted between the two types.
In our diagram, primitive classes show up as another entity that straddles the line between primitive values and value objects, alongside the basic primitives and their boxes:
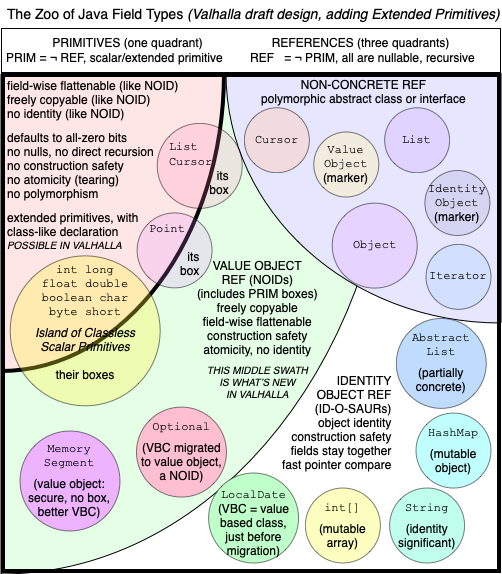
Values of type int, double, etc., allow for boxing conversion to the wrapper class types, and unboxing conversion back to the primitive types. Similarly, an instance of a primitive class supports value object conversion to the class’s reference type, and primitive value conversion back to the class’s primitive type. Like unboxing, a primitive value conversion will fail on an attempt to convert null.
All classes declare a superclass type (Object by default) and a list of superinterface types. These types set up a subtyping (is-a) relationship between the class’s reference type and the supertypes (we write A <: B to indicate A is a subtype of B). For a primitive class, the primitive type is monomorphic, but the reference type has the expected subtyping relationship.
This means that if we declare:
primitive UnsignedShort extends Number
implements Comparable<UnsignedShort> {
...
}then UnsignedShort.ref <: Number, and UnsignedShort.ref <: Comparable<UnsignedShort>. To assign an UnsignedShort to the type Number, it first undergoes value object conversion to type UnsignedShort.ref, and then the normal subtyping rules apply.
The instanceof operator, pattern matching, and reflection work primarily with classes, not types. So we can reasonably ask a Number if it is an instance of class UnsignedShort; and when we ask for its class, we may get UnsignedShort.class.
UnsignedShort us = ...
Number n = us;
if (n instanceof UnsignedShort) {
assert n.getClass() == UnsignedShort.class;
}While primitive types are not subtypes of reference types, we can introduce a new relationship based on extends / implements clauses, which we’ll call extends. We’ll say A extends B means A <: B when A is a reference type, and A.ref <: B when A is a primitive type. The relation is also reflexive: A extends A for all types.
Arrays
Arrays of reference types are covariant; this means that if A <: B, then A[] <: B[]. This allows Object[] to be the “top array type”, at least for arrays of references. But arrays of primitives are currently left out of this story.
We can unify the treatment of arrays by defining array covariance over the new “extends” relationship; if A extends B, then A[] <: B[]. This means that for a primitive P, P[] <: P.ref[] <: Object[], making Object[] the top type for all arrays.
Of course, if a Point[] is-a Object[], this means it has to support reading and writing of references, even though the array actually stores primitive values. Value object conversions (on reads) and primitive value conversions (on writes) are thus dynamically applied, as needed, to support the appropriate physical encodings. Attempting to store a null in a primitive array will cause the primitive value conversion to fail.
Default values
Fields and array components are always initialized to their default value before a program has a chance to read or modify them. For reference types, this value is null. But because primitive types cannot be null, the default value of a primitive class’s primitive type is the class’s initial instance — an instance with all field values set to their own default values.
The basic primitives (int, double, etc.) reflect the design assumption that zero is a reasonable default. If we choose to model an entity with a primitive class, we are making the same assumption: that the zero representation is a reasonable default.
For some abstractions, such as LocalDate, there is no reasonable default other than null. If we choose to represent a date as the number of days since some epoch, there will invariably be bugs that stem from uninitialized dates; we’ve all been mistakenly told by computers that something will happen on or near 1 January 1970. Even if we could choose a default other than the zero representation, an uninitialized date is still likely to be an error. For this reason, LocalDate is better suited to being a value class than a primitive class — because not only is zero not a reasonable default, it has no reasonable default.
The choice to use a zero default instead of null was one of the central tradeoffs in the design of the basic primitives. It gives us a usable initial value (most of the time), and requires less storage footprint than a representation that supports null (int uses all 2^32 of its bit patterns, so a nullable int would have to either make some 32 bit signed integers unrepresentable, or use a 33rd bit). This was a reasonable tradeoff for the basic primitives, and is also a reasonable tradeoff for many other potential primitive types (such as complex numbers, 2D points, half-floats, etc.).
Tearing
For the primitive types longer than 32 bits (long and double), it is not guaranteed that reads and writes from different threads (without suitable coordination) are atomic with respect to each other. The result is that, if accessed under data race, a long or double field or array component can be seen to “tear”, where a read might see the low 32 bits of one write, and the high 32 bits of another. (Declaring the containing field volatile is sufficient to restore atomicity, as is properly coordinating with locks or other concurrency control.)
This was a pragmatic tradeoff given the hardware of the time; the cost of atomicity on 1995 hardware would have been prohibitive, and problems only arise when the program already has data races — and most numeric code deals with thread-local data. Just like with the tradeoff of nulls vs. zeros, the design of primitives permits tearing as part of a tradeoff between performance and correctness, where primitives chose “as fast as possible” and objects chose more safety.
Today’s JVMs give us atomic loads and stores of 64-bit primitives, because the hardware makes them cheap enough. But primitive classes bring us back to 1995; atomic loads and stores of larger-than-64-bit values are still expensive, leaving us with a choice of “make operations on primitives slower” or permitting tearing when accessed under race. For the new primitive types, we choose to mirror the behavior of the existing primitives.
Just as with null vs. zero, this choice has to be made by the author of a class. For classes like Complex, all of whose bit patterns are valid, this is very much like the choice around long in 1995. For other classes that might have nontrivial representational invariants, the author may be better off declaring a value class, which offers tear-free access because loads and stores of references are atomic.
Legacy primitives
As part of generalizing primitives, we want to adjust the basic primitives (int, double, etc.) to behave as consistently with new primitives as possible. We can start by declaring int as a primitive class, with methods and supertypes. This class has a special keyword for a name, but otherwise can behave like a standard primitive class.
We can’t change the fact that existing code wants to refer to int value objects with type Integer, but we can treat Integer as an alias for the more uniform spelling int.ref. Then the legacy wrapper class Integer can be replaced by the primitive class int (assuming all its public methods are preserved in the new class).
Why a reference type at all?
It is sensible to ask: why do primitive classes need a reference type at all? The need for reference companions is analogous to the need for boxes in 1995: we’d made one set of tradeoffs for primitives, favoring performance: they are non-nullable, their default is zero, they can tear under race, they are unrelated to Object, etc. Most of the time, we ignored the box types, but sometimes we needed to temporarily suppress one of these properties, such as when interoperating with code that expects an Object. The reasons we needed boxes in 1995 still apply to primitive classes: most of the time, we will deal with them as primitives, but sometimes we need the affordances of references (nullability, non-tearability under race, polymorphism, self-reference), and in those cases, we appeal to the reference type. The expectation is that using P.ref will be about as rare as using Integer explicitly today.
Reasons we might have to appeal to the reference type include:
-
Interoperation with other reference types. If primitive classes can implement interfaces and extend classes (including
Objectand some abstract classes), then some class and interface types are going to be polymorphic over both identity and value objects. This polymorphism is achieved through object references — a reference toObjectmay be a reference to an identity object, or a reference to a value object. -
Nullability. Nullability is an affordance of object references, not objects themselves. Most of the time, it makes sense that primitive types are non-nullable (as the primitives are today), but there may be situations where
nullis a semantically important value. UsingP.refwhen nullability is required is semantically clear, and avoids the need to invent new sentinel values for “no value.”This need comes up when migrating existing classes. The method
Map::getusesnullto signal that the requested key was not present in the map — but if theVparameter toMapis a primitive class,nullis not a valid value. We can capture the “Vornull” requirement by changing the descriptor ofMap::getto:public V.ref get(K key);where, whatever type
Vis instantiated as,Map::getreturns the reference companion. (For a typeVthat already is a reference type, this is justVitself.) This captures the notion that the return type ofMap::getwill either be a reference to aV, or thenullreference. (This is a compatible change, since both erase to the same thing.) -
Self-referential types. Some types may want to directly or indirectly refer to themselves, such as the “next” field in the node type of a linked list:
class Node<T> { T theValue; Node<T> nextNode; }We might want to represent this as a primitive class, but then the layout of
Nodewould be self-referential, and since we want to flatten primitives into the layout of their enclosing types, this would lead to an infinite regress. The solution is to explicitly opt for a reference, where we can usenullto indicate that there is no next node:primitive class Node<T> { T theValue; Node.ref<T> nextNode; } -
Compact arrays. Some algorithms have a sequential access pattern that works best on flat arrays of bare values while others, with a random access pattern, work better on arrays of true references to separately buffered values. In the latter case, a compact array of type
P.ref[]might perform better. (This is a subtle choice that typically needs validation from benchmarks!) Depending on the relative sizes of barePvalues and managed references, and depending on the algorithm, one array type or the other might use less memory bandwidth. -
Protection from tearing. We may want to use the reference type when we are concerned about tearing. We can use
P.refas a field or array component type to request reference semantics; because loads and stores of references are atomic,P.refis immune to the tearing under race thatPmight be subject to. (Thevolatilemodifier offers an alternative solution for fields, but comes with some additional, possibly unwanted performance implications. Some race-accepting multithread algorithms might work better with safely bufferedP.refvalues than with bareP.) -
Consistency with existing boxing. Autoboxing is convenient, in that it lets us pass a primitive where a reference is required. But boxing affects far more than assignment conversion; it also affects method overload selection. The rules are designed to prefer overloads that require no conversions over those requiring boxing (or varargs) conversions. Having both a primitive and reference type for every primitive class means that these rules can be cleanly and intuitively extended to cover new primitives.
Bringing primitives and objects closer together
While primitives and objects still have some differences, we can dramatically reduce the size of the table of differences we started with. Rather than identity being a property of all objects, identity becomes a property objects can opt into — and the semantics of == follows from that choice. Both primitives and objects can be declared using classes. We can give primitives members, supertypes, and array covariance. Which leaves us with a much smaller set of differences:
| Primitives | Objects |
|---|---|
| Not nullable; default value is zero | Nullable; default value is null |
| Tearable under race | Initialization safety guarantees |
| Convertible to polymorphic objects | Polymorphic |
Value classes vs. primitives
It is reasonable to ask, why would we introduce two new forms of declaration, value classes and primitive classes? Couldn’t one or the other be good enough?
While we could of course get away with only one of these (we’ve been getting away with neither for 25 years), whichever one we picked would be unsatisfying for some of the desired use cases. If we picked value classes only, new numeric types would be burdened by the requirement to represent nulls (which has a footprint cost) and to manage atomicity of loads and stores. If we picked primitives only, it would be very tempting to use primitives even when they are not entirely appropriate, and users would be stuck with an inconvenient default value or with objects that cannot protect their invariants when accidentally shared under a data race. There’s a reason for the remaining rows in our primitives-vs.-objects table; sometimes you want nulls, and sometimes not; sometimes you can tolerate tearing to get maximum performance, and sometimes not.
How would we choose between declaring an identity class, value class, or primitive? Here are some quick rules of thumb:
-
Use identity classes when we need mutability, layout extension, or locking.
-
Consider value classes when we don’t need identity, but need nullity or have cross-field invariants.
-
Consider primitives when we don’t need identity, nullity, or cross-field invariants, and can tolerate the zero default and tearability that comes with primitives.
-
Remember that the
P.refreference type for a primitive recovers the benefits of a value class.
Regarding performance we can observe some complementary rules of thumb:
-
Identity objects usually live in the heap, except on a very good day with JIT inlining and escape analysis.
-
Value objects should tend to stay above the heap as arguments and returns, but buffer in the heap when their references are stored there.
-
Bare primitive values should appear in the heap less as separately buffered objects and more as flattened values in their containers.
Summary
Valhalla unifies, to the extent possible, primitives and objects. The following table summarizes the transition from the current world to Valhalla.
| Current World | Valhalla |
|---|---|
| All objects have identity | Some objects have identity |
| Fixed, built-in set of primitives | Open-ended set of primitives, declared with classes |
| Primitives don’t have methods or supertypes | Primitives have classes, with methods and supertypes |
| Primitives have ad-hoc boxes | Primitives have regularized companion reference types |
| Boxes have accidental identity | Value objects have no identity |
| Boxing and unboxing conversions | Value object and primitive value conversions, but same rules |
| Primitive arrays are monomorphic | All arrays are covariant |